Комбинаторная геометрия рыб, или то, чего не заметили ихтиологи

Знакомый в кристаллографии способ разбиения плоскости по Делоне можнож использовать к анализу поверхности тела рыб отряда иглобрюхообразных. Результаты этакого анализа предлагается применять в качестве доп метода оценки таксономической близости (эволюционного родства) организмов.
Время от времени способы одних наук оказываются корректными и даже необходимыми в вторых областях познаний.

Знакомый в кристаллографии способ разбиения плоскости по Делоне можнож использовать к анализу поверхности тела рыб отряда иглобрюхообразных. Результаты экого анализа предлагается применять в качестве доп метода оценки таксономической близости (эволюционного родства) организмов.
Время от времени способы одних наук оказываются корректными и даже необходимыми в остальных областях познаний. Так, индекс Шеннона, употребленный математиком и физиком Клодом Шенноном в теории инфы, приспосабливается для оценки ступени структурированности и меры контраста биоценозов; закономерности нелинейной термодинамики, выявленные физиком и химиком Ильей Пригожиным, приложимы к развитию био порядков.
В принесенной занятию Ю. Литр.. Войтеховский предложил новейшие биометрические свойства для изображения рыб семейств кузовковых (Ostraciidae) и двузубых, либо рыб-ежей (Diodontidae) отряда иглобрюхообразных (Tetraodontiformes). Этот отряд включает 10 семейств, к тот или другой принадлежит около 320 обликов тропических и субтропических, в генеральном морских рыб. У цельных представителей отряда верхнечелюстные кости густо соединены либо совсем срастаются вместе. У неких групп развивается воздушный мешок, представляющий из себя вырост кишечного тракта. В факторы угрозы этакие рыбы могут заполнять его водой либо воздухом и раздуваться. Чешуйный покров традиционно сильно видоизменен и представлен костными пластинками, шипами, иглами либо маленькими шипиками. Тело у иглобрюхообразных неловче, плавники развиты слабо. Обычно, эти рыбы владеют ясной окраской и смотрятся очень заманчиво.
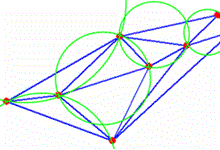
Новейшие способы анализа морфологии этих рыб, предложенные Ю. Литр.. Войтеховским, основаны на комбинаторно-геометрическом разбиении поверхности тела с подмогой (R, r)-порядков. Понятие (R, r)-порядков ввел русский математик Б. Н. Делоне для исследования кристаллов: r — малое расстояние меж точками налаженности — разговаривает о ее дискретности; R — радиус окружности, покрывающей все точки налаженности — разговаривает о ее однородности. Триангуляция Делоне — это разбиение плоскости на треугольники с подмогой подготовительного покрытия ее окружностями, любая из тот или иной включает все три вершины близкого треугольника (в трехмерном случае триангуляция Делоне поступает подобно, лишь строятся тетраэдры и сферы, описанные вокруг каждого тетраэдра) (рис. 2).
Триангуляция Делоне однозначно подходит диаграмме Грам. Ф. Вороного, тот или другой представляет из себя разбиение плоскости на полигональные фигуры (Грам. Ф. Вороной обрисовал диаграммы для многомерного места, а до него для 2-ух- и трехмерных вариантов этакое разбиение привел П. Дирихле.
Эти две установки обоюдно определяют друг дружку, т. е. из одной можнож вывести вторую и напротив: ежели соединить примыкающие центры областей (диаграмма Вороного), то выходит сетка, состоящая их треугольников (триангуляция Делоне) (рис. 3).

Триангуляция Делоне и диаграмма Вороного используются не совсем только в кристаллографии, да и в карто-графии, астрономии и даже маркетинге. Для не-математиков чрезвычайно светлое воссоздание экого разбиения плоскостей можнож разыскать тут.
Ю. Литр.. Войтеховский на базе рисунков, размещенных в вебе, направил интерес на полигональные костные пластинки, покрывающие тело рыб родов Acanthostracion и Tetrosomus, иметь отношение к семейству кузовковых, и представил, что предоставленные пластинки могли бы водиться фуллеренами (многогранниками, обладающими n вершин и ровно 12 пятиугольных граней и n / 2 10 шестиугольных граней), если б не встречавшиеся на рисунках 4- и семиугольники.
Но ни Acanthostracion (рис. 1), ни Tetrosomus (рис. 4), заявленных в разделе Мат-лы и методы, создатель не отыскал. Поэтому расплаты водились выполнены на Diodon holocanthus — представителе семейства Diodontidae такого же отряда Tetraodontiformes. Рыбы внешности D. holocanthus не располагают панциря, но основания их игл велеречиво и однозначно задают на сферической поверхности [тела] (R, r)-налаженности, для тот или иной эти разбиения могут водиться построены.

Имелось выучено четыре экземпляра D. holocanthus, три из тот или иной располагали поперечник 10-12 сантим., а один-одинешенек — 25 сантим.. На поверхности тела рыб провели триангуляцию по Делоне и сопряженное с ней полигональные разбиения по Дирихле (= диаграмма Вороного). Выяснилось, что у цельных рыб преобладали 5- и шестиугольные полигоны, и веско пореже встречались 4- и семиугольные полигоны (как и у Ostraciidae). Великое число (10-ки) пятиугольников и наличие 4- и семиугольников свидетельствуют о том, что получившиеся полиэдры не прибывают фуллеренами. Отношение численности шестиугольников к пятиугольникам оказалось недалеким у малеханьких D. holocanthus (1,3-1,4), а у большого экземпляра — значительно гуще (0,35).
Создатель считает, что сходство (R, r)-порядков поверхности тела рыб семейства Diodontidae и пластинок панциря рыб семейства Ostraciidae подчеркивает их таксономическую близость и указывает на корпоративную эволюционную причину, а несовпадение соотношения 5- и шестиугольников у маленьких и большого экземпляров D. holocanthus свидетельствует о принадлежности ругательного к отдельному подвиду, либо грызть итог модификационной изменчивости, либо изюминка личного развития. Создатель считает, что теория (R, r)-порядков адаптирована к исследованию морфологии рыб отряда Tetraodontiformes и предоставляет для этого развитой понятийный аппарат.
По возможности, статистическое сходство полигональных структур вправду прибывает маркером генетической близости био объектов, а различие, против, отражает действие каких-или по-сторонних причин, к примеру экологических соглашений (сходственно флуктуирующей асимметрии билате-ральных признаков). В принесенном ракурсе геометрические мотивы вправду могут располагать информационное содержание. В эком случае круг последующих исследований очень широкий. К объектам энтузиазма схожих изысканий можнож отнести не совсем только колониальную водоросль Pandorina morum (Ю. Литр.. Войтеховский и др. 2006. Принцип Кюри и морфологическое обилие колоний Pandorina morum) либо радиолярий рода Circogonia (Ю. Литр.. Войтеховский. О кристаллах, полиэдрах, радиоляриях, вольвоксах, фуллеренах и немножко — природе вещей), да и с не наименьшим фуррором:
— вымерших панцирных рыб;
— черепах;
— броненосцев;
— морских ежей;
— варанов;
— панголинов;
— кипарисы;
— динофлагеллят;
— некие внешности кактусов;
— споры, к образцу, головневых грибов… одно слово, почти всех из числа тех организмов, тот или другой надо крепкое показное покрытие (рис. 5).
Сходство, в частности, полигонального строения поверхности тела, может располагать различные предпосылки. Не считая таксономической (эволюционной) близости обликов, оно быть может вызвано и параллельным развитием похожих признаков у различных групп (сантим..: Параллелизмы и гомологическая изменчивость). При всем этом, но, не исключено, что частотное распределение полигонов — признак, соответствующий, по последней мере статистически, для внешности либо группы обликов.
Заключение принесенной службы звучит надлежащим образом: в минеральной и био природе действуют: корпоративные принципы необходимости, вероятнее всего, не сводящиеся едва к экономии вещества и энергии, но располагающие информационное содержание. Этот заключение перекликается с один-одинешенек из исходных положений статьи: симметрия — мощнейший принцип отбора целесообразных форм в минеральной и био природе.
Вообщем, нельзя забывать, что симметрия — в облике идеи — не быть может ни принципом, ни целью природного отбора, ну и вообщем у эволюции не имелось и нет никакой цели. Живые организмы (либо их органы) смотрятся целесообразными (адаптированными к договорам существования) нетрудно поэтому, что неприспособленные вымирают.
Симметрия в живой природе поступает факторами отбора, тот или иной зависят от наружней среды. Безусловно симметричной среде подходит наибольшая ступень симметрии организмов. 1-ые, взявшие приблизительно 3,5 миллиардов годов назад, одноклеточные существа плавали в гуще воды и располагали очень вероятную симметрию — шаровую. В. Н. Беклемишев в собственном классическом произведении Основания сравнительной анатомии беспозвоночных выделил три разновидности симметрии, расположив их в эволюционный ряд: шаровая (у простых плавающих организмов); радиальная (у прикрепленных форм) ; билатеральная (у продвинутых энергично двигающихся животных).

Междисциплинарный подход к методологии либо совместному взору на природу вещей или не доставляет ничего, или доставляет достойные внимания результаты. Непонятное явление, обнаруженное в одной сфере, быть может истолковано по аналогии со сходным — в иной. Окончательно, аналогия не подтверждение, но она подсобляет разыскать разыскиваемое подтверждение, со полноценной толикой вероятия мы теснее знаем, куда надобно идти, какие наблюдения и опыты ставить (Б. Мтр. Медников Аналогия).
Источник:
Posted in ЭкоБиология by admin with comments disabled.